Dashboard

Vyn's Blog

AE-GAN Optimizations

April 20, 2022

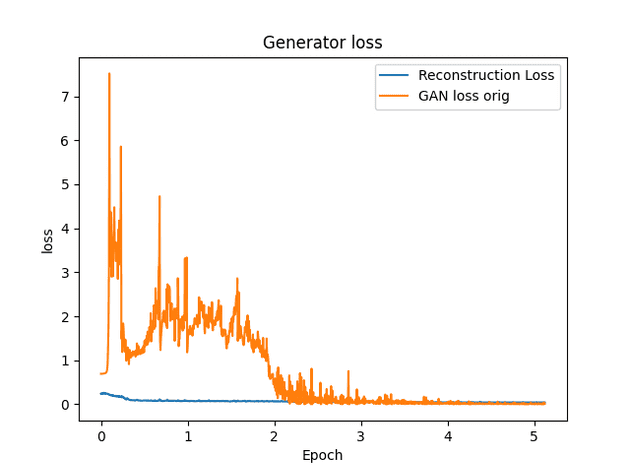
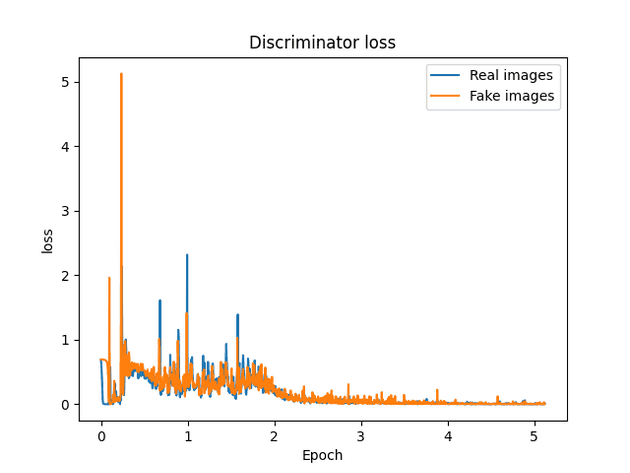
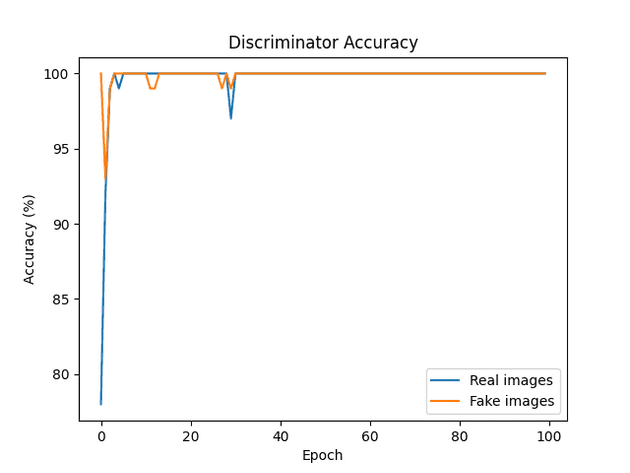
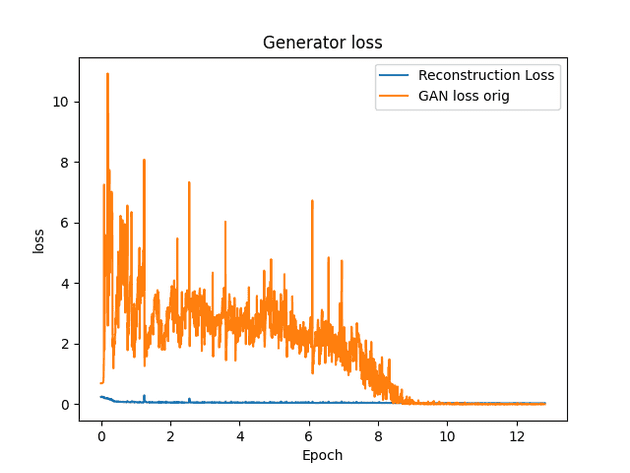
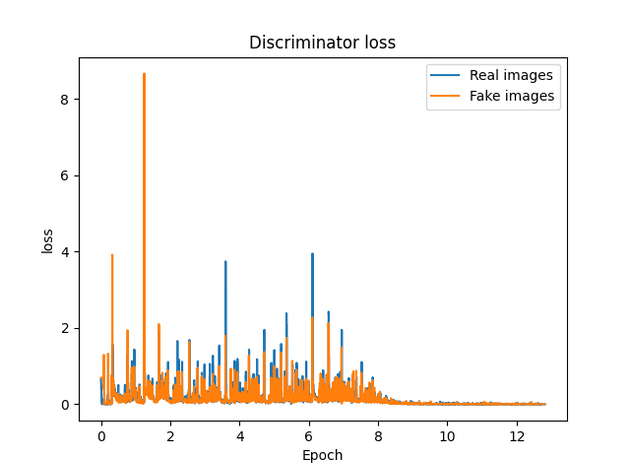
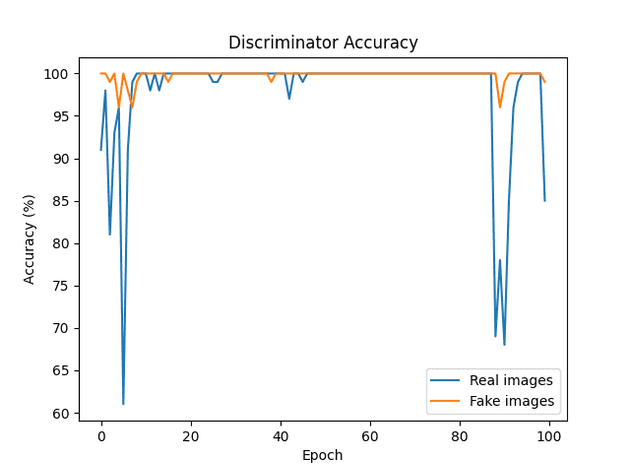
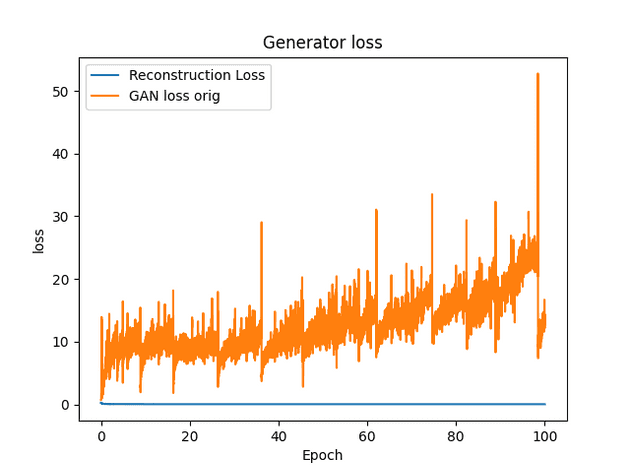
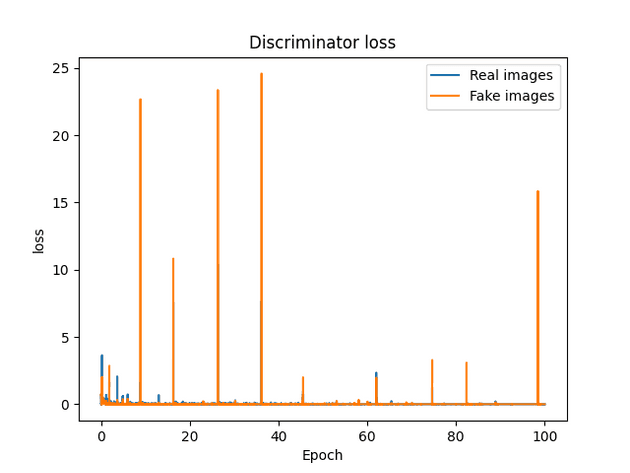
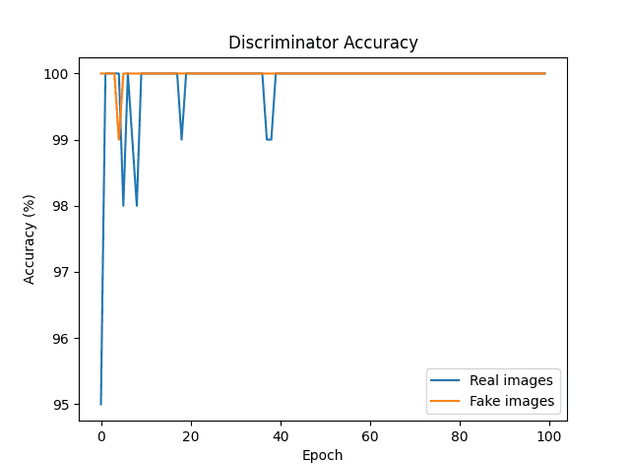
AE-GAN version 1

Changes from previous model (test model from last week)

New loss function

  • Want GAN loss to increase as AE loss decreases.
  • Do this by scaling the GAN loss by 1 / AE loss.
  • Need 0.0005 scalar multiplier in order to keep GAN loss the same order of magnitude as AE loss.
def loss_wapper(g_model, alpha, beta):
    mse = MeanSquaredError()
    bce = BinaryCrossentropy()

    def loss(x, y_true, y_pred):
        # run data through generator
        y = g_model(x)
        # calculate typical loss functions
        ae = mse(x, y)
        gan = bce(y_true, y_pred)

        # scale ae loss and invert
        ae_loss = tf.math.scalar_mul(alpha, ae)
        ae_loss_inverted = 1 / ae_loss

        # gan_loss should = gan_loss * 0.0005 * (1/ae_loss) Hopefully that will allow recovery from convergence f ailure
        gan_loss_scaled = tf.math.scalar_mul(beta, gan)
        gan_loss = tf.math.multiply(gan_loss_scaled, ae_loss_inverted)
        # record results for analysis
        with open(f"./{MODEL_NAME}/data/alpha_beta_loss_{MODEL_NAME}.csv", "a") as f:
            f.write(f"{ae},{gan}\n")

        return ae_loss + gan_loss

    return loss

Batch size

  • Changed from 128 to 256. This makes 195 batches per epoch since dataset is 50,000 images.

Results

Observations

  • Smiles seem to change slightly. This is probably due to the generative characteristics of the model.
  • Faces have slight changes that are not necessarily reconstructions.
  • Images are still relatively blury, (see metrics section).

Data

aegan inverse1 generator loss aegan inverse1 discriminator loss aegan inverse1 discriminator accuracy

Vector Arithmetic

Top row: smiling women (last column is average latent vector output)

Middle row: neutral women

Bottom row: neutral men

Last image: smiling women - neutral women + neutral man aegan inverse1 vector arithmetic

AE-GAN version 4

Changes from previous model (version 1)

New loss function

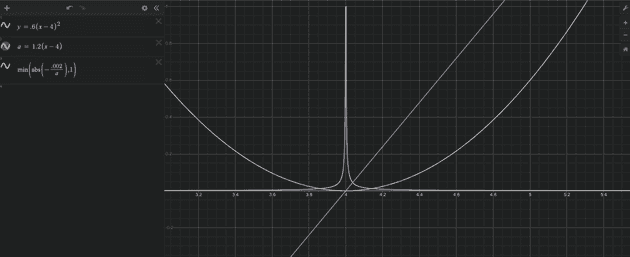
The idea behind this loss function was to make the gan loss beta value increase as the derivative of ae loss approaches 0. As the derivative approaches 0, the idea is that the ae process is nearing completion the closer the derivative gets to 0. Additionally, if the derivative becomes positive, the beta scalar will decrease the same as it increased. The graph below shows a parabolic curve, representing the ae loss value over time. The purple line is the derivative and the spiky line is the negative inverse of the derivative. In practice, ‘a’ (the inverse scalar value) had to be adjusted to tune the steepness of the curve.

derivative graph 

def loss_wapper(g_model, alpha):
    mse = MeanSquaredError()
    bce = BinaryCrossentropy()

    def loss(x, y_true, y_pred):
        # run data through generator
        y = g_model(x)
        # calculate typical loss functions
        ae = mse(x, y)
        gan = bce(y_true, y_pred)

        # Read previously stored loss data
        df = pd.read_csv(f"./{MODEL_NAME}/data/alpha_beta_loss_{MODEL_NAME}.csv")
        beta = 0
        # calculate derivative over the last 50 batches
        if len(df.index) > 50:
            derivative = df["ae_loss"].diff(periods=50) / df[
                "ae_loss"
            ].index.to_series().diff(periods=50)
            # calculate scaled negative inverse
            beta_vec = abs(-0.0000002 / derivative)
            # limit max beta to 1
            beta_vec = beta_vec.apply(lambda x: min(x, 1)).fillna(0)
            beta = beta_vec.iloc[-1]

        gan_loss_scaled = tf.math.scalar_mul(beta, gan)
        # record results for analysis
        with open(f"./{MODEL_NAME}/data/alpha_beta_loss_{MODEL_NAME}.csv", "a") as f:
            f.write(f"{ae},{gan},{beta}\n")

        return ae + gan_loss_scaled

    return loss

Results

Observations

  • Eyes are much more prominent on these images. I think that is due to the GAN loss being more active in this model.
  • Images are still pretty blury.

Data

aegan inverse4 generator loss aegan inverse4 discriminator loss aegan inverse4 discriminator accuracy

Vector Arithmetic

Top row: smiling women (last column is average latent vector output)

Middle row: neutral women

Bottom row: neutral men

Last image: smiling women - neutral women + neutral man aegan inverse4 vector arithmetic

AE-GAN version 5

Changes from previous model (version 4)

New loss function

def loss_wapper(g_model, alpha):
    mse = MeanSquaredError()
    bce = BinaryCrossentropy()

    def loss(x, y_true, y_pred):
        # run data through generator
        y = g_model(x)
        # calculate typical loss functions
        ae = mse(x, y)
        gan = bce(y_true, y_pred)

        gan_ceil = min(ae, gan)

        # record results for analysis
        with open(f"./{MODEL_NAME}/data/alpha_beta_loss_{MODEL_NAME}.csv", "a") as f:
            f.write(f"{ae},{gan}\n")

        return ae + gan_ceil

    return loss

Results

Observations

  • Results are almost identical to the baseline model.

Data

aegan inverse5 generator loss aegan inverse5 discriminator loss aegan inverse5 discriminator accuracy

Vector Arithmetic

Top row: smiling women (last column is average latent vector output)

Middle row: neutral women

Bottom row: neutral men

Last image: smiling women - neutral women + neutral man aegan inverse5 vector arithmetic

Metrics

Metric Baseline AE-GAN version 1 AE-GAN version 4 AE-GAN version 5
Blur factor (dataset raw = 658.269) 112.923 102.538 232.115 114.730
Discriminator loss real 1.0542e-12 4.697e-10 2.069e-8 1.316e-12
Discriminator loss fake 1.308e-9 0.0 0.0 1.959e-10
Discriminator accuracy real 100% 99.650% 97.800% 99.870%
Discriminator accuracy fake 99.950% 99.880% 99.800% 99.990%
Generator loss 0.694 0.017 0.017 0.707
Complexity (trainable/non-trainable) 3,222,587 / 1,651,841 3,222,587 / 1,651,841 3,222,587 / 1,651,841 3,222,587 / 1,651,841
Latent space nodes 100 100 100 100

Conclusions